Continuous-Discrete Node Value Transfer Function¶
The Continuous-Discrete node Value Transfer function (CDVT function) is available in Analysis Menu under the Network Menu. In essence the CDVT function implements a modelling technique to circumvent the limitation of no discrete children of continuous nodes in CLG Bayesian networks. A discrete interval node is linked to a continuous node such that the expression generating the distribution of the discrete node is equal to the posterior marginal of the parent continuous node. In this way the discrete node becomes a discretize representation of the continuous node. The discrete node has no table as the table is regenerated using the Table Generator functionality. The states of the discrete node are determined by the user prior to compiling the network. Remember to add -infinity and infinity as lower- and upper limits in the discrete interval node.
Figure 1: The dashed arrow specifies a CVDT function link.¶
Figure 1 shows a link between a continuous and discrete nodes pair created by the CDVT function.
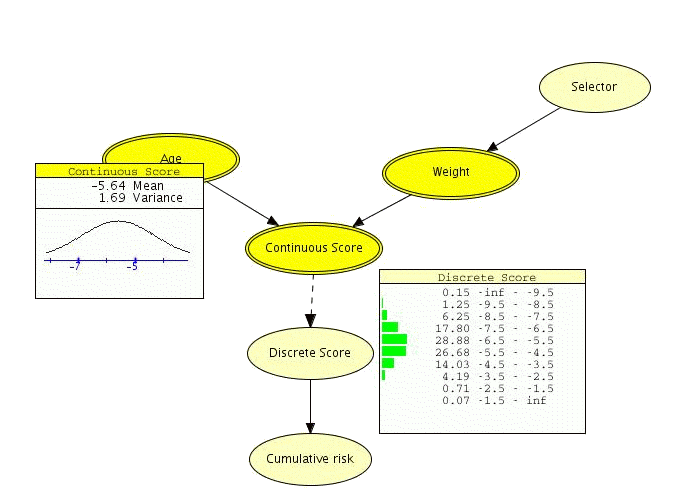
Figure 2: The Discrete Score is a discrete approximation of the Continuous Score computed using Table Generator functionality.¶
Figure 2 illustrates how the density function of a continuous node can be approximated by a discrete distribution using the CDVT function.
The CDVT function has some major limitations such as evidence can only be propagated along the direction of the CDVT link, only sum-normal equilibrium is supported and no type of analysis is supported on a network with CDVT links.
The discretization link should be used with extreme care.