Distance Analysis Dialog

Interaction with the Dialog

Figure 1 shows the distance analysis dialog as it appears after being activated. In dialog the distance between a pair of Network Models can be measured. The models subject to analysis must be loaded before activating the dialog. Whether the model needs to be in runtime mode depends on the selected measurement method. The text area is used for output. If the dialog succeeds in calculating a measure, the configuration and result will written here.

Figure 1: The Correlation Analysis Dialog.

Select the input parameters:

• M1 and M2 are the models used in the analysis. Choices are among the loaded Models.

• Measure is the measuring method used in the analysis. The available distance measures and additional details can be found under Available Measures below.

The dialog will attempt to perform a distance calculation as soon as any input parameter has been changed. In case one of the models is not in the required mode, the dialog will inform about this inside the result text area below. Also, in case the measurement method encounters incompatible node types or any other limitation a message will also appear in the result text area.

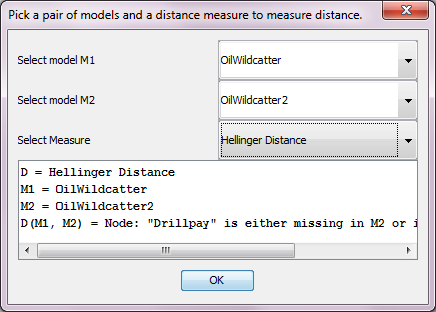
Figure 2: The out put will provide indications of any error or any encountered limitation.

Available Measures

Hellinger Distance

Requirements and Limitations

The Hellinger Distance measures the distance between 2 Bayesian Network Models: M1 and M2. Identical Variables are recognized in M1 and M2 by names of variables. Nodes with identical names in M1 and M2 must have the same number of states. Only discrete chance nodes are allowed. Hellinger Distance works for models both in edit mode and i run mode.

The Hellinger Distance between two probability distributions P and Q is defined as:

\[D_H (P, Q) = \sqrt{\sum_{i} \sqrt{p_i} - \sqrt{Q_i}}\]

Weighted Hellinger Distance

Requirements and Limitations

The Weighted Hellinger Distance measure has the same requirements and Limitations as Hellinger Distance exept that it requires models to be in runmode.

In the Weighted Hellinger Distance: \(D^{w}_{H} (P_1 (X| \pi), P_2(X| \pi))\), the Hellinger Distance \(D_{H} (P_1 (X| \pi), P_2(X| \pi))\) is weighted by the probability of the parent configuration \(P( \pi)\).