Adaptation Tutorial¶
Adaptation is the process of refining the (conditional) probabilities specified for a Bayesian network by taking into consideration real experiment outcomes or cases. For example, assume we have a Bayesian network relating the causal relationships between a set of diseases and a set of symptoms. Every time a patient is diagnosed, the information about his/her symptoms and the diseases he/she is suffering from can be used to adapt the network’s probabilities. Using the HUGIN Graphical User Interface, we can adapt a network by using experience tables and/or fading tables. Below is a detailed discussion of how to perform adaptation in the HUGIN Graphical User Interface, including an overview of the computations performed. The mathematics is presented for those who want to get a deeper understanding of the adaptation process and can be skipped without any discontinuity in the reading. The Adaptation Algorithm is well-suited for sequential parameter update whereas the EM Algorithm is well-suited for parameter estimation in batch (i.e., estimation of the parameters of conditional probability tables from a set of cases).
Experience Tables In Adaptation¶
Experience Tables are used to specify prior experience on the parameters of the conditional probability distributions. Notice that adaptation is disabled for nodes without an experience table and parent configurations that have a zero experience count.
Example of Adaptation¶
We use the example from the Experience Tables to illustrate the use of adaptation. The Bayesian network is shown in Figure 1. download Chest Clinic to learn more about the domain of this network.
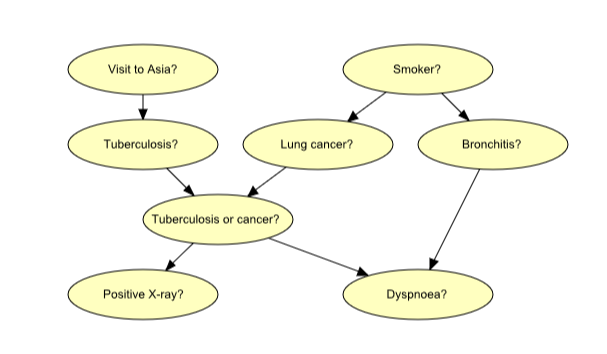
Figure 1: Bayesian-network representation of “Chest Clinic”.¶
The conditional probability distribution (represented by a conditional probability table (CPT)) of the variable Smoker (S) prior to any adaptation is (0.5,0.5). We assume that the experience count for Smoker has been set to 10 as in the example. Now compile the network, enter the observation (evidence) that variable S is in state 0 (“yes”), and click the adaptation button . Click the adaptation button four more times, denoting that this observation has been made five times.
Figure 1: The adapdation option.¶
Now, if we reinitialize the network, we will see that the CPT of variable S has changed from (0.5,0.5) to (0.667,0.333). Also, all the variables that are not independent of S have different probability distributions. In general, the CPTs of the variables ancestral to the observed variables may be updated when the adaptation button is clicked, provided their experience tables exist and the counts are greater than zero. Note that deleting or resetting the experience tables does not affect the CPTs of the variables.
To understand why the values have changed, it’s easier to see the experience table again. If we go to Edit Mode and see the experience table for the “Smoker?” variable, we will see that the current experience count is 15, corresponding to an initial count of 10 and having made 5 observations of the variable. Before adaptation began we had an experience count of 10, and the probability distribution was (0.5,0.5), i.e., 5 of them were “yes”; and the other 5 were “no”.
The additional 5 counts all pertain to state “yes”. Therefore, the adapted probability distribution of “Smoker?” becomes
where N(“x”) denotes the number of times we experienced state “x”. The result agrees with the values we saw. Below is a definition of adaptation, which gives a concise description of what we have been doing so far.
To summarize, an adaptation step consists of entering evidence, propagating, and updating (adapting) the conditional probability tables and the experience tables.
To make the experiments specified below, please close the network file, and choose “No” when the Hugin Graphical User Interface shows the prompt to save the file, so that we can begin with the original file.
In the network of Figure 1, it is justified to add experience tables to all the variables in the domain except for “Tuberculosis or cancer”, since this variable is a logical OR and no experience can be gained on logical OR variables. After we have added experience tables to all variables (by choosing “Add Experience Table to All Discrete Chance Nodes”), we have to modify the experience counts because they are initially all zero. In our case, we add experience tables to all variables in the network (except the “Tuberculosis or cancer” variable) and set the initial experience counts to 10. The network is now ready for adaptation.
The experience table of a variable represents the experience counts of the parent configurations, as mentioned earlier. Figure 3 shows the CPT and the experience table for “Has Bronchitis”.
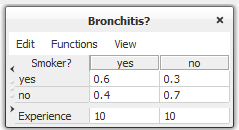
Figure 3: The CPT and experience table for “Has Bronchitis” before adaptation.¶
The interpretation of Figure 3 is that we have observed the value of the “Has Bronchitis” 20 times, 10 of them when “Smoker?” was in state “yes” and 10 when “Smoker?” was in state “no”. Combining this information with the CPT of “Has Bronchitis”, we can get information about the initial experience of each individual state. Since there are 10 observations of “Has Bronchitis” when “Smoker?” was in state “yes” and
we have
where we have used a new notation for N to conform with conditional probability notation. Similarly, for Smoker?=”no” we have
giving the total individual state experience counts of
and .. math:: N(“No”) = 20 - 9 = 11.
With these values we can now compile the network and do some adaptation. Adaptation requires at least one variable with an experience table in order to adapt the network. Note that it is not necessary to have non-zero experience counts or to enter identical experience counts for every parent configuration. For instance, the initial experience counts could be set to “10,0”. Note also that we don’t have to worry about the computations which we have been doing so far, as they are only intended for users who want a deeper understanding of the adaptation process.
Let’s say we have observed five cases for which
Variable S (Smoker?) is in state 0 (“yes”)
Variable B (Has Bronchitis) is in state 0 (“yes”)
Then propagate this evidence. Next click the adaptation button five times as we have done before. Each time the adaptation button is clicked the probability of this observation increases. Now reinitialise the network and observe the conditional probability distribution of “Smoker?” as we did before. As before, the conditional probability distribution has changed from (0.5,0.5) to (0.667,0.333) since the adaptation we just performed is the same as before in the context of variable “Smoker?”. As for “Has Bronchitis?”, the new CPT and the updated experience table is shown in Figure 4.
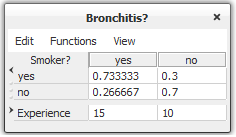
Figure 4: The CPT and experience table for “Has Bronchitis” after adaptation.¶
The right hand columns of Figures 3 and 4 (i.e., P(Has Bronchitis = “yes” | Smoker? = “no”) and P(Has Bronchitis = “no” | Smoker? = “no”)) haven’t changed. This is because in all the five adaptation steps that we ran, evidence was entered that variable “Smoker?” was in state “yes”, giving no new information about the states of “Has Bronchitis” when the state of “Smoker?” is “no”. We can see similar information also from Figure 4, where the experience under “yes” has increased by 5 while the one under “no” remained the same.
On the other hand, the left side column (i.e., P(Has Bronchitis = “yes” | Smoker? = “yes”) and P(Has Bronchitis = “no” | Smoker? = “yes”)) has changed, showing that some experience has been gained. Using the above results from the computation before adaptation was performed, we have
agreeing with the results displayed in the HUGIN Graphical User Interface.
Fading Tables¶
The adaptation procedures we have gone through so far gave equal weight to recent experiences and older ones (that is why we were just adding and dividing as if they were observations done at the same time). Often, however, old observations do not count as much as more recent ones. Thus we have to unlearn or forget some of them. This is the same as saying that new observations (evidence) are more important than older evidence and hence should have more weight in the adaptation process. We can make HUGIN respond to such situations by using fading tables.
Fading tables are meaningless without experience tables (i.e., in order to forget something we must have had remembered it first). In order to implement fading, we have to introduce a fading factor, which is the rate at which previous observations are forgotten. A fading factor of 0 means that there is no adaptation and a fading factor of 1 means there is no fading.
The following is a description of how to use fading tables in the HUGIN Graphical User Interface and how they work. Close the network we have been working with so far without saving it or adjust the experience counts to 10 and set the conditional probabilities back to (0.5,0.5). The steps needed to add a fading table to a variable are similar to those for adding an experience table to the variable. To add a fading table to a discrete chance variable select the variable, do a right click, and select “Add Fading Table” in the “Experience/Fading Table Operations” submenu. Then select “Show fading table” item of the View menu of the node table for the “Smoker?” node and enter the fading factor in the fading table section of the node table. The fading factor should be a number between 0 and 1. If we enter 0 or a number greater than 1, no matter how many times we try to adapt the network, nothing will change. If we choose 1, it will work as if there was no fading taking place. Note that if a variable does not have an experience table, then it is not possible to add a fading table to the variable. For this example, enter a fading factor of 0.5 to the “Smoker?” variable. Now enter the evidence that Smoker? is in state 0 (“yes”). Click the adapt button once and switch to Edit Mode to see the updated CPT and experience table of “Smoker?”. The results are shown in Figure 5.
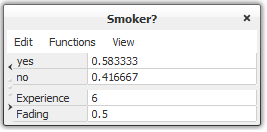
Figure 5: The CPT, experience table, and fading table for “Smoker?” after adaptation.¶
One thing that you might have noticed is that the experience count has decreased from 10 to 6. How come the experience count decreased while we were adding some experience to the network? To explain this, let’s consider the fading factor. After one adaptation run the experience counts and probabilities can be computed as
where we again use the somewhat informal N notation. N(previous_yes) and N(previous_no) are the previous experience counts in the “yes” and “no” states respectively and N(experience) is the total experience count for the concerned variable. To add fading tables to all discrete chance variables in the network click the right mouse button somewhere in the Network Pane, choose “Add Fading Table to All Discrete Chance Nodes” in the “Experience/Fading Table Operations” submenu, and add the fading factor for each variable.